The goal of this article is to compare the HLL sketch implemented in this library to Druid’s original HyperUnique aggregator sketch.
The starting point in this comparison was a choice of parameter K=2048 for HLL sketch in such a way that it would approximately match the size of Druid HyperLogLogCollector, which has no parameters available to the user. It is quite difficult to measure the size of a Java object in memory, therefore the serialized size was used as the best available measure of size, which is also important for many practical applications in large systems.
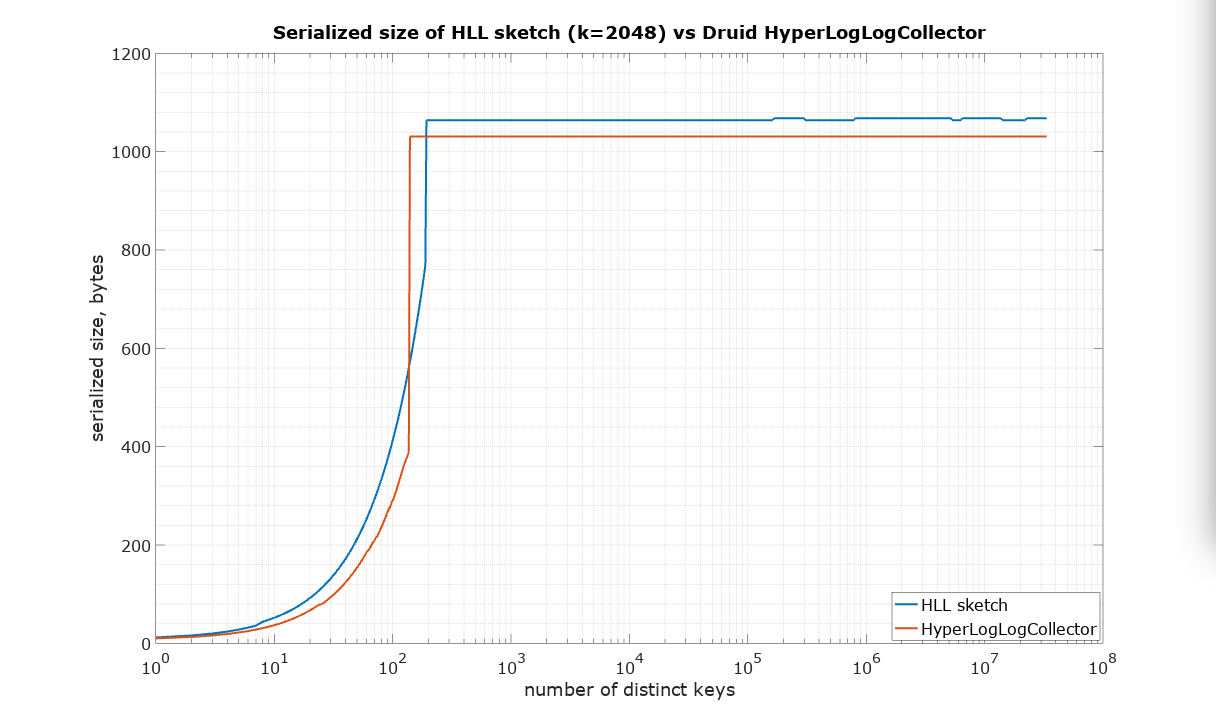
The following plots are what we call pitch-fork plots. The X-axis is the number of distinct identifiers presented to the sketch. The Y-axis is the relative error plotted as +/- percent where values above zero represent an overestimate and values below zero represent an underestimate.
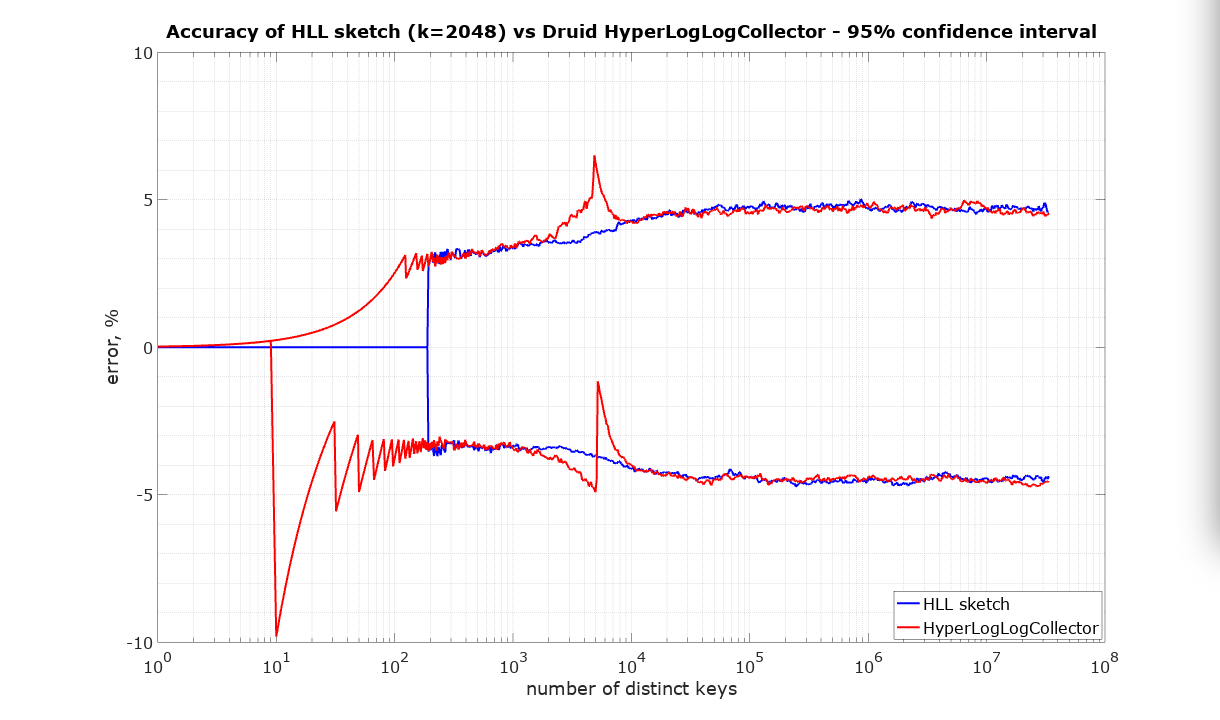
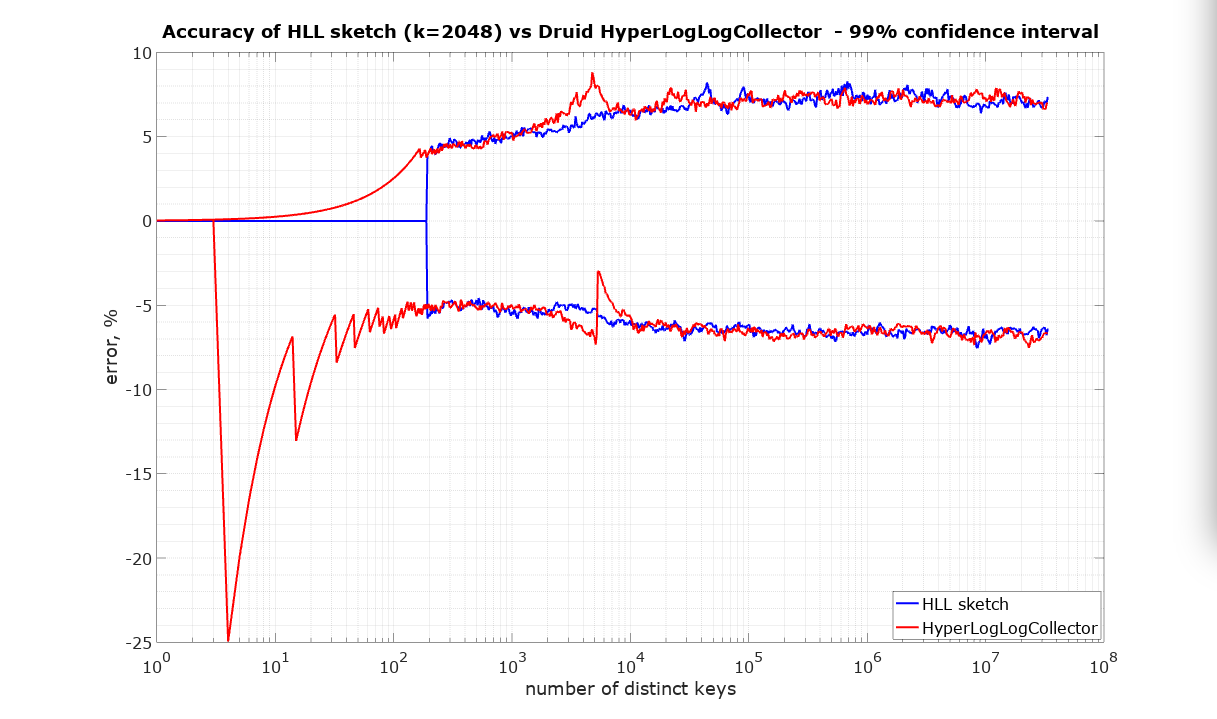
The HLL algorithm is fully mergeable. In simple terms this means that there should be no penalty for partitioning the input, processing these partitions separately, and finally merging the resulting sketches. The resulting estimate is required to be at least as accurate as if the whole input had been presented to a single sketch.
It was proved in Flajolet’s HLL paper that for sufficiently large N and K, the standard error (i.e. the normalized RMS error) of HLL should be 1.0389 / sqrt(K), whether or not any merging has occurred. This guarantee works out to be about 2.3% when K = 2^11.
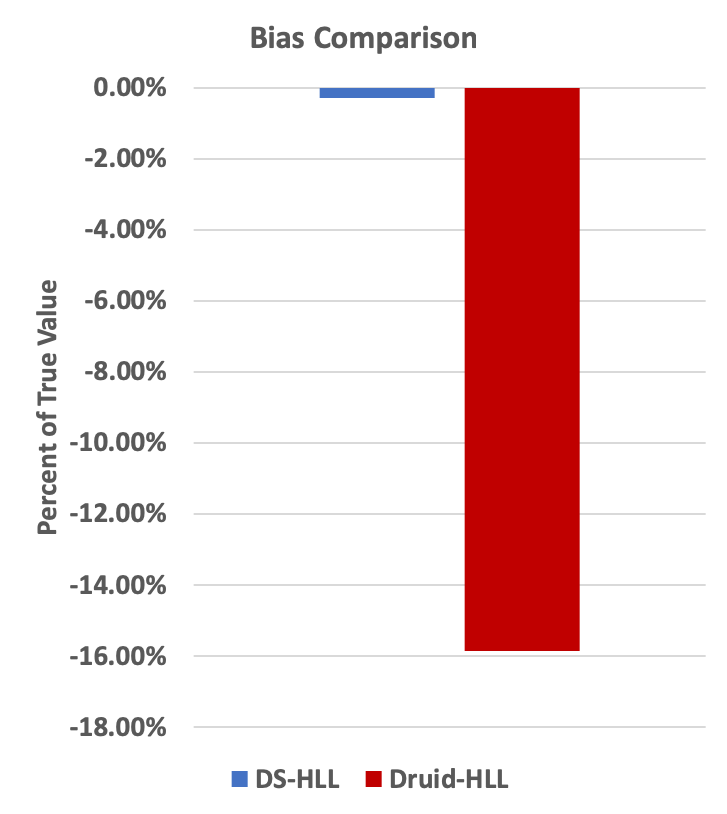
The following is an empirical demonstration that the library’s implementation of HLL exhibits the required behavior after merging, but Druid’s implementation of HLL does not. The latter’s measured standard error is about 7 times larger than HLL’s theoretical guarantee. This is mostly due to bias; on average, Druid is undercounting by about 16 percent on this example.
The test consisted of 100 trials of merging 8192 sketches into a single sketch. Each of the input sketches had been updated with 32768 unique values. The error is computed
Sketch Size: lgK = 11, k = 2048 True count: 2.68435456E8
Distinct keys per sketch = 32768
Number of sketches = 8192
Number of trials = 100 RSE Specification for this size sketch = 1.03896 / SQRT(2^11) = 0.023 = +/- 2.3% at 68% confidence.
The DataSketches library HLL implementation:
Mean estimate: 2.6826835125572532E8 (0.06 percent low, essentially no bias!)
Normalized RMS Error: 0.021226565654784535 (better than the RSE Specification)
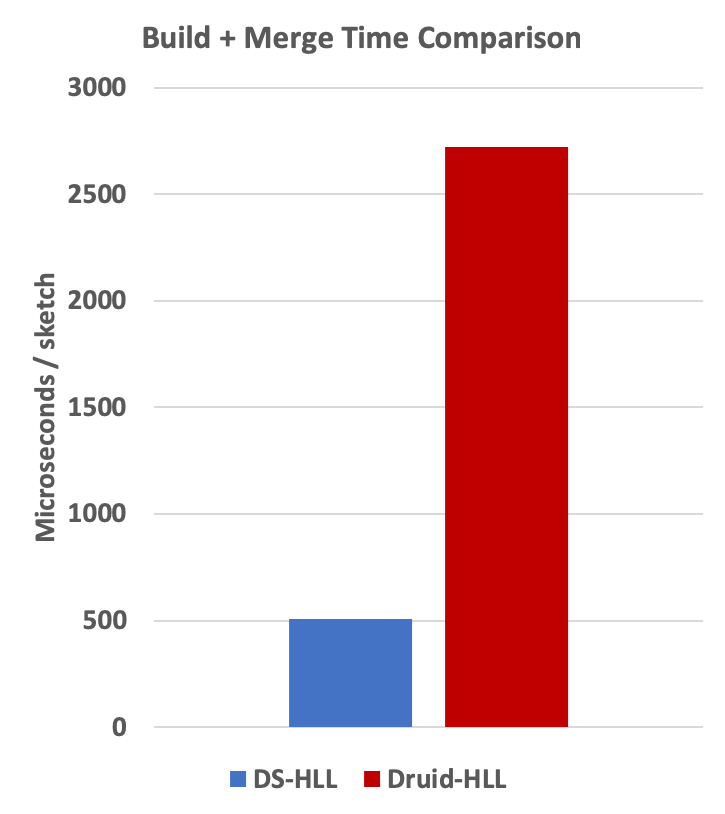
Total Job Time : 0:07:33.241
The Druid HLL implementation:
Mean estimate: 2.2560974267493743E8 (16 percent low)
Normalized RMS Error: 0.16058739888244847 (7 times the RSE Specification)
Total Job Time : 0:36:43.451
Also, Druid’s implementation was much slower.
The above comparisons can be visualized in the following charts:
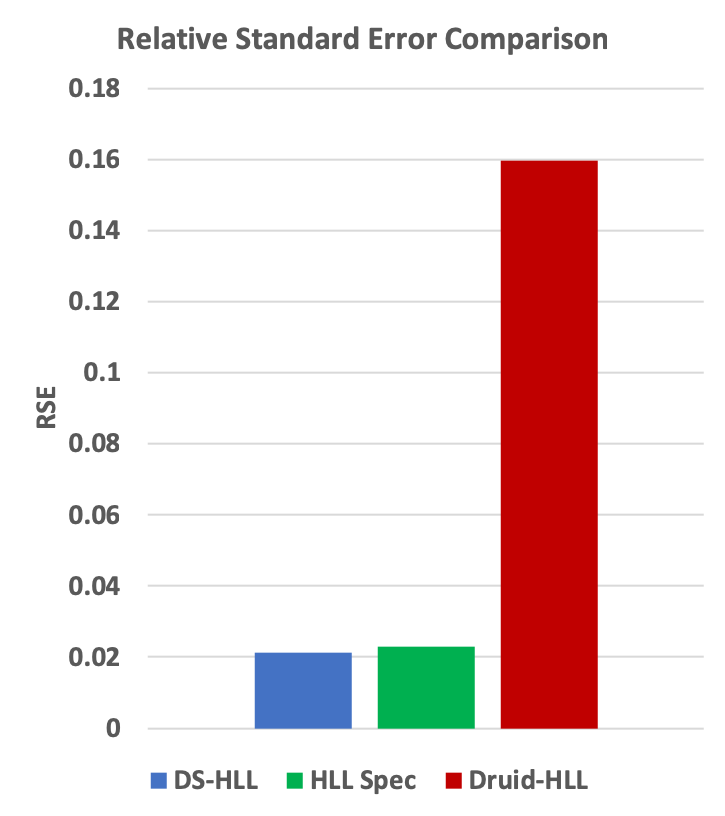
Technical Note: the library’s HLL sketches are more complicated than the standard HLL algorithm. In certain special cases where better-than-HLL accuracy is possible, the library employs other estimators, and even other stochastic processes and data structures. When those special cases no longer apply, the library falls back to the standard HLL estimator algorithm. One of these special cases is for a simple streaming sketch that is not involved in merge operations we can take advantage of a more advanced estimator algorithm with improved error properties. When comparing the error of a merged sketch to the error of a non-merged sketch, the library’s HLL sketches will have a slightly larger error after merging. This is the direct result of this fall-back mechanism. This slightly larger error is still within the RSE Specification of error defined as 1.03896 / SQRT(k).
The code to reproduce these measurements is available in the Datasketches/characterization repository
The DataSketches Hll sketch module for Druid is available as a part of Druid/Extensions-core